Economics (NCERT) Notes
Topics
All
Civil Services in India (26)
Ethics, Integrity and Aptitude
» Chapters from Book (11)
» Case Studies (8)
Solved Ethics Papers
» CSE - 2013 (18)
» CSE - 2014 (19)
» CSE - 2015 (17)
» CSE - 2016 (18)
» CSE - 2017 (19)
» CSE - 2018 (19)
» CSE - 2019 (19)
» CSE - 2020 (19)
» CSE - 2021 (19)
» CSE -2022 (17)
» CSE-2023 (17)
Essay and Answer Writing
» Quotes (34)
» Moral Stories (18)
» Anecdotes (11)
» Beautiful Poems (10)
» Chapters from Book (5)
» UPSC Essays (40)
» Model Essays (38)
» Research and Studies (4)
Economics (NCERT) Notes
» Class IX (14)
» Class X (16)
» Class XI (55)
» Class XII (53)
Economics Current (51)
International Affairs (20)
Polity and Governance (61)
Misc (77)
Select Topic »

Civil Services in India (26)
Ethics, Integrity and Aptitude (-)
» Chapters from Book (11)
» Case Studies (8)
Solved Ethics Papers (-)
» CSE - 2013 (18)
» CSE - 2014 (19)
» CSE - 2015 (17)
» CSE - 2016 (18)
» CSE - 2017 (19)
» CSE - 2018 (19)
» CSE - 2019 (19)
» CSE - 2020 (19)
» CSE - 2021 (19)
» CSE -2022 (17)
» CSE-2023 (17)
Essay and Answer Writing (-)
» Quotes (34)
» Moral Stories (18)
» Anecdotes (11)
» Beautiful Poems (10)
» Chapters from Book (5)
» UPSC Essays (40)
» Model Essays (38)
» Research and Studies (4)
Economics (NCERT) Notes (-)
» Class IX (14)
» Class X (16)
» Class XI (55)
» Class XII (53)
Economics Current (51)
International Affairs (20)
Polity and Governance (61)
Misc (77)

2.6 Price Ratio and the Slope of the Budget Line
Price Ratio and the Slope of the Budget Line
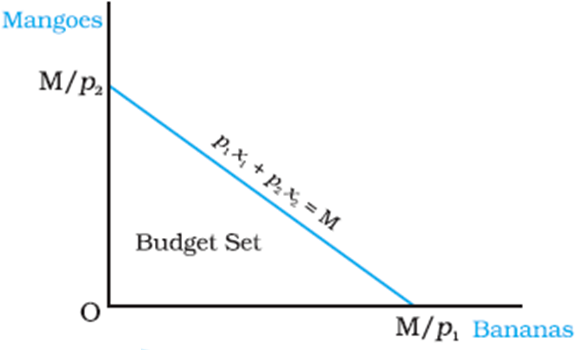
•Any point on the budget line represents a bundle which costs the consumer her entire budget.
•If the consumer wants to have one more banana (cost p1) , she can do it only if she gives up some amount of the other good mangoes (cost p2)
•If the consumer wants to have an extra quantity of bananas when she is spending all her money, she will have to give up p1/p2 quantities of mangoes.
•The equation of line is p1x1 + p2x2 = M
•Hence, x2=M/p2-(p1/p2)x1
•If the number of banana is creased by 1 (x1 +1)
•The number of Mangoes would be x’2= M/p2-(p1/p2)*(x1 +1)
•Hence, x’2= (-) p1/p2
•In the given market conditions, the consumer can substitute bananas for mangoes at the rate p1/p2
•Absolute value of p1/p2 is to be taken since the numbers has to be integer
•The absolute value of the slope of the budget line measures the rate at which the consumer is able to substitute bananas for mangoes when she spends her entire budget.
Changes in the Budget Set
•The set of available bundles depends on the prices of the two goods and the income of the consumer.
•When the price of either of the goods or the consumer’s income changes, the set of available bundles is also likely to change.
•Suppose the consumer’s income changes from M to M’ but the prices of the two goods remain unchanged.
With the new income, the consumer can afford to buy all bundles (x1, x2) such that p1x1 + p2x2 ≤ M’
•x2=M’/p2-(p1/p2)x1
Effect of Change of Income
•Here the slope of the new budget line is the same as the slope of the budget line prior to the change in the consumer’s income.
•However, the vertical intercept has changed after the change in income.
•If there is an increase in the income,the vertical as well as horizontal intercepts increase, there is a parallel outward shift of the budget line and consumer can buy more of the goods at the prevailing market prices.
•If the income goes down, both intercepts decrease, and hence, there is a parallel inward shift of the budget line and the availability of goods goes down.
Changes in the Set of Available Bundles of Goods Resulting from Changes in the Consumer’s Income
Effect of Change in prices
•If the price of bananas change from p1 to p'1 but the price of mangoes and the consumer’s income remain unchanged, the consumer can afford to buy all bundles (x1,x2) such that p’1x1 + p2x2 ≤ M
•The equation of the budget line is p’1x1 + p2x2 = M
•x2=M/p2-(p’1/p2)x1
•Hence, the vertical intercept of the new budget line is the same as the vertical intercept of the budget line prior to the change in the price of bananas.
•However, the slope of the budget line and horizontal intercept have changed after the price change.
Changes in the Set of Available Bundles of Goods Resulting from Changes in the Price of bananas.
•If the price of bananas increases, the absolute value of the slope of the budget line increases.
•If the price of bananas decreases, the absolute value of the slope of the budget line decreases.
| Related Articles |
| Recent Articles |
